1.数组-简单-找到所有数组中消失的数字

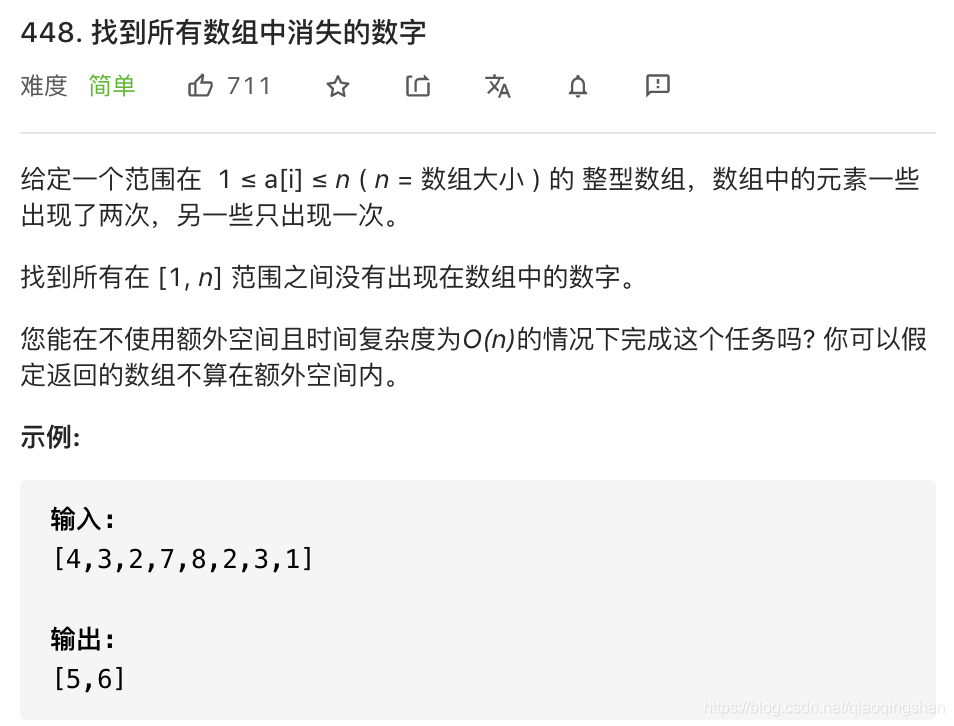
这道题的收获就是又重温了一下基本概念，空间复杂度和java里面list的使用。

本题思路简述

这个题的难点主要就是在于实现自己编写代码空间复杂度O(1)，时间复杂度（n）。通过空间复杂度的要求，可以看出，最好我们自己不要再开辟一个新的数组了，就用题目中已经给的nums数组会比较好一些。

主要思路就是对nums进行遍历，将里面每一个数字对应的i进行加n操作，然后再重新进一遍遍历，看看数组里哪一个i对应的nums[i]是小于n的，如果小于，那么就是我们需要的答案。

需要注意的就是，为了避免遍历的时候，当时的数字已经执行了+n操作，所以需要对每一个数字进行%n操作，还原回原来的数字。

2.数组-简单-买卖股票的最佳时机

2.1思路提点

这个题用两种方法求解的，一种利用了动归思想，一种利用了暴力求解思想。
本质上就是求数组里前后两个数之差的最大值。（注意，一定是一前一后）

2.2思路简述

1.动态规划思路
用这个思路的话，主要的点就是要设立两个值min，max来进行记录
其中，min值记录的是到当前数组i的位置之前区域的最小值
Max值记录的是利润最大值。
每次遍历的时候，执行两个判断：
1.min=Math.min(min.nums[I]);
2.max=Math.max(max,nums[I]-min);

最后返回max就可以啦

2.暴力求解思路
简单粗暴，就是计算出数组里每两个前后数字之差。但是会超时
核心代码. max=Math.max(max, mums[j]-nums[I]);

3.数组-简单-多数元素（求众数）

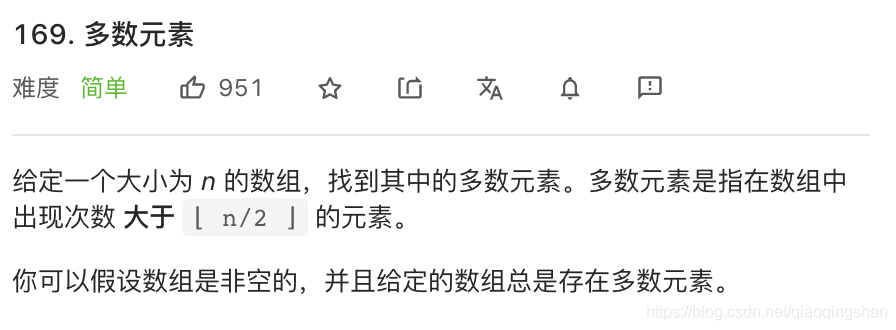
3.1 思路提点

首先说一下，这道题里面学到了怎么在java里面调用排序；
就是用Arrays.sort( )这个方法；
另外就是学到了摩尔投票法这个方法。

3.2 思路简述

1一种比较简单的方法-排序法

主要思想就是将数组先进行排序，因为这个题目说了，一定存在出现次数超过半数以上的数字，所以排序之后的数组，中间的那个数，一定就是众数。
用Arrays.sort（）这个方法。

2.进阶方法-摩尔投票法

其主要思想就是用投票的方法来进行判断，如果有相同的，就计数+1，视为投赞成票，如果不相同，则计数-1。如果计数减为0，那么就换一个数，再进行以上的计数模式。

因为多数元素的个数-其余元素的总个数》=1
所以抵消到最后肯定还剩余至少一个多数元素。

3.3 求众数2（进阶版）

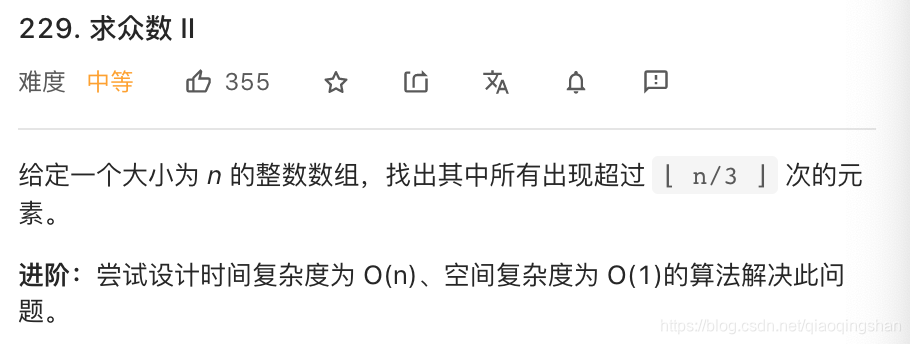
这道题和上一道最大的区别就是从选一个众数变成了选两个最多数。
怎么说呢，要找到其中所有出现超过n/3的数，那么最多只存在两个数满足，因为三个数都超过n/3的话，那么就超过1了，明显不可能。
所以此时就将候选者设置为2个，用上一题的方法来用其他的数和这两个数进行对比，如果相同则加1，如果不同则减1。如果此时count为0，则替换候选者后再将count置一。

而且需要注意的是，在选出两个候选者之后，必须重新对他们进行计数验证，看看是不是真的大于1/3，如果确定是，那么就加入list。
此题结束。

下面是一个小小的总结。

4.数组-简单-最大子序和

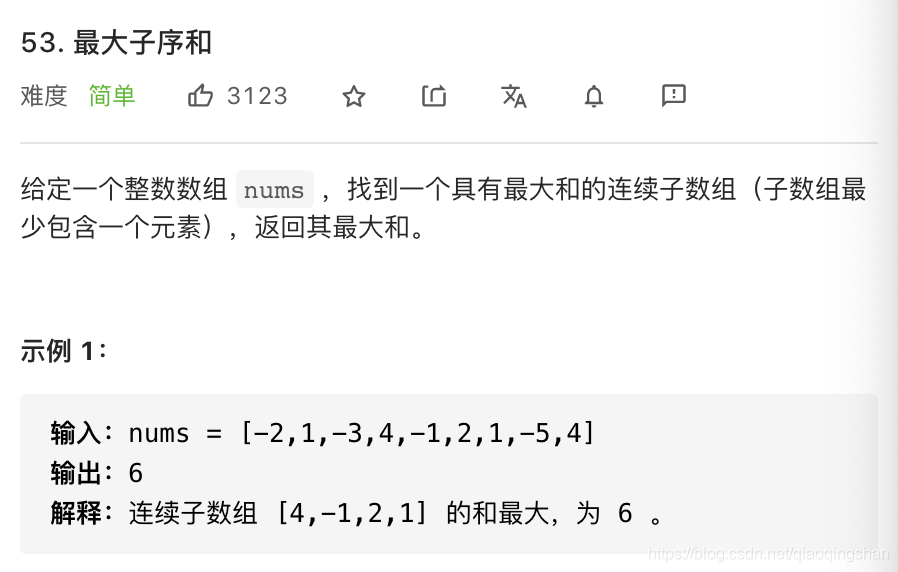
题解：这道题主要就是运用了动态规划的思想。
它的核心思路就是设立dp[ ]数组，来记录如果截止到nums数组里的各元素i时，在nums[0]到nums[i]这一段区域里连续子数组的最大和。(⚠️，这里是指这一段区域一定以元素i为最后一个)
即，dp[3]，存储的就是nums数组里0-3这一块区域里连续子数组的最大和，也就是4自己一个数组，其和为4.

计算dp数组里的值的具体方法思路如下所示：

dp[0]的值也就是第一个数的值；
dp[1]=max（dp[0],0）+nums[1];

同理
Dp[I]=max(dp[i-1],0)+nums[i];

在计算dp数组的数值时，时刻进行比较，选出dp数组里最大的那一个，就是我们需要的最大值啦，是不是很简单呢。

5.数组-简单-两数之和

这个题解的关键就在于应用HashMap。map的key指的数值，value指的该数值在传入里数组排第几（即数组下标）
解题的主要思路，就是在map数组里面查看是否有key，其值等于targer减去nums[i]，如果有的话，就反回其value和i，也就是两个数的数组下标。
然后就解决啦！

6.数组-简单-移动零

比较简单的一个解题思路：设立两个指针，一个j，在初始数组str1里面进行循环，一旦发现不是0的数，就放到另一个数组array里面。然后指针j定格到所有非0数字的最后一个，也就是得到了所有非0数据的个数。
然后将str1剩余个数都设置为0就可以了。

另外一个解题思路，主要就是借鉴的快速排序的思路。
同样设置两个指针i，j，如果i当前值是等于零的，那么j不动，i++；
如果i当前值不等于零，那么i，j进行交换，j++，i++；
本质就是要保证j左边的数都是非零的。

本质是一个循环不变量：在每一次循环前，j 的左边全部都是不等于0的

• 起始j为0，明显满足
• 此后每一次循环中，若nums[i] = 0，则j保持不变，满足；若nums[i] != 0，交换后j增一，仍然满足